Explicación de Integrales inmediatas

Recordatorio

• Definición de primitiva:
  Las primitivas de una función $F\left(x\right)$ se representan por
  
  $$\int F\left(x\right)dx$$
  Son el conjunto de funciones $f\left(x\right)$ cuyas derivadas son iguales a $F\left(x\right)$. Es decir, $f\left(x\right)$ es una primitiva de $F\left(x\right)$ si $f^{\prime }\left(x\right)=F\left(x\right)$.
  
  Hablamos en plural ya que, por ejemplo, $f\left(x\right)=x^2+1$ y $g\left(x\right)=x^2+2$son dos primitivas distintas de $F\left(x\right)=2x$.
  Nótese que la diferencia entre ambas primitivas es sólo una constante. Por ello, cuando calculamos una integral, siempre escribimos la constante de integración $K$:
  
  
  El símbolo $\int$ se denomina signo integral y $dx$ indica que la variable de integración es 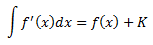$x$.

Ejemplos:

$$\int 2yxdx=y{x}^2+K$$

$$\int 2yxdy=y^{2}x+K$$

En la primera integral, tratamos la $y$ como una constante, integrando respecto de $x$. En la segunda, es al contrario.

Propiedades de las integrales:

• Integral de una Suma
  
  
  Es decir, la integral de la suma de dos funciones es la suma de las integrales de ambas funciones.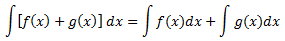
• Producto por una constante
  
  
  Es decir, las constantes (números o parámetros; o factores que no sean función de x) salen fuera de la integral multiplicándola.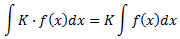
  Esta propiedad será útil tanto de izquierda a derecha como de derecha a izquierda, pues en ocasiones necesitamos en el integrando un número en concreto para aplicar la regla de la cadena, por lo que multiplicaremos y dividiremos la integral por este número y, aplicando la propiedad, podemos introducir el factor que multiplica (o rl que divide) en el integrando.